2024年8月4日更新:图床跑路,所有图片均丢失
0x0 洛必达是什么
对于洛必达法则,维基百科是这样介绍的:
洛必达法则(法语:Règle de L’Hôpital,英语:L’Hôpital’s rule)是利用导数来计算具有不定型的极限的方法。该法则以法国数学家纪尧姆·德·洛必达的名字命名,但实际上是由瑞士数学家约翰·伯努利所发现。
借助一个简单的例子,我们可以轻松了解什么是洛必达法则:
例 0-1
对于函数 $f(x)=\frac{ln(x)}{x-1}$ ,求$\lim_{x \to 1}f(x)$的极限。
通过简单的取特殊值描点连线,我们可以得到该函数的图像:
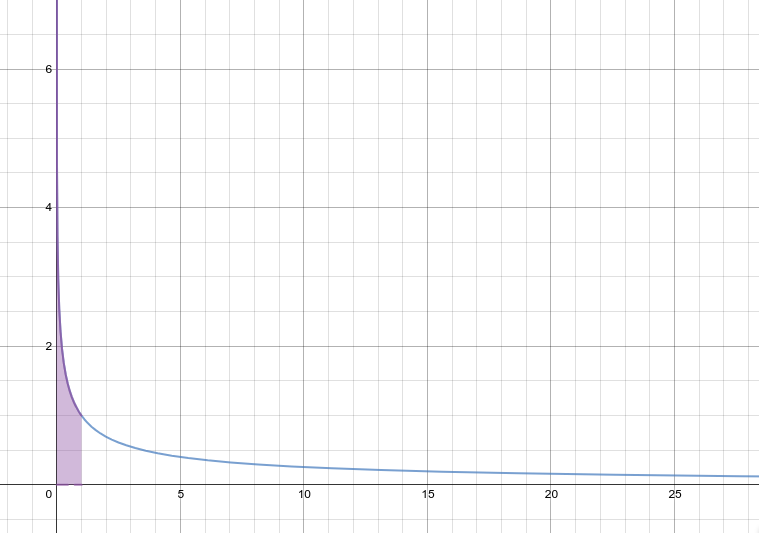
当我们试图将$x=1$代入函数式时,我们会发现,分母$x-1$在此时等于$0$,明显地,这是有悖于我们的常识,分母是不能为$0$的那么我们该如何解决这个问题呢?
现在我们将分子和分母拆分来看,分别得到函数式和图像:
$$
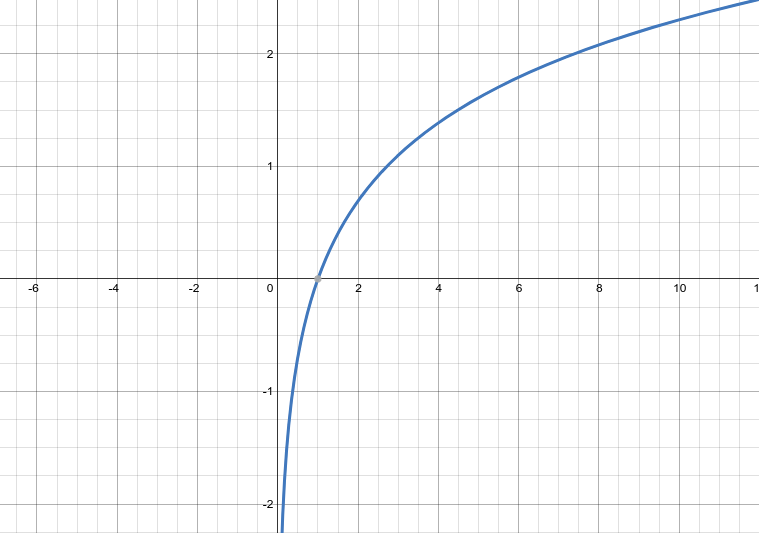
g(x)=ln(x)
$$
$$
h(x)=x-1
$$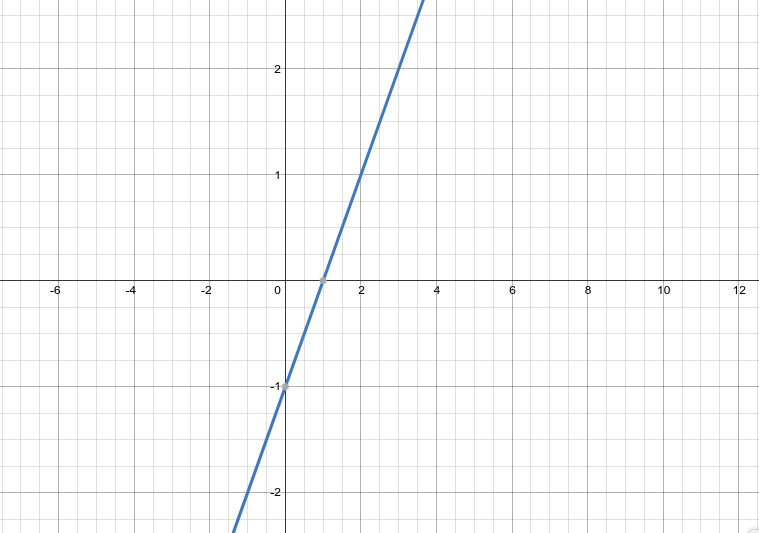
不难发现,函数$g(x)$和$h(x)$均过点$(1,0)$,故我们将其无限放大,由于两者均为可微函数,且可微函数局部是线性的,因此二者的无限放大图像均为直线。
回想我们曾经学到的关于
斜率的定义,可以意识到,在这种极限情况下,我们可以将极限处的斜率作为函数值使用,故可得:$$
lim_{(x\to 1)}f(x)=lim_{(x\to 1)}\frac{g(x)}{h(x)}=lim_{(x\to 1)}\frac{g’(x)}{h’(x)}=lim_{(x\to 1)}\frac{\frac{1}{x}}{1}=1
$$
0x1 洛必达法则的局限性
- 分子分母同时趋向于$0$($\frac{0}{0}$)或同时趋向于$\infty$($\frac{\infty}{\infty}$)
- 分子分母在限定的区域内是否分别可导。
- 高考不可用(Doge)
0x2 洛必达法则在高中阶段的例题实战
例2-1
当$x>0$时,不等式$e^x {\geq} ax+1$恒成立,求实数$a$的取值范围。
解答:
分离参数得$a{\leq}\frac{e^x-1}{x}$,其中$a>0$
令$f(x)=\frac{e^x-1}{x}$,对其求导得
$f’(x)=\frac{(x-1)e^x+1}{x^2}$,令$g(x)=(x-1)e^x+1=0$
得$x=0$
对$g(x)$求导,得$g’(x)=xe^x$,当$x>0$时,$g’(x)>0$
因此$g(x)$在$x>0$时单调递增
要求$a\le f(x)$恒成立,因此$a\le f(x)_{min}$,但当$x=0$时,$e^x-1=x=0$,此即为$\frac{0}{0}$型不定式。根据洛必达法则,有:
$\lim_{x \rightarrow 0}{\frac{e^x-1}{x}}=\lim_{x \rightarrow 0}{\frac{e^x}{1}}=1$,因此$a\le 1$,实数 a 的取值范围是$(-\infty ,1]$。
0x3 课后习题
若不等式$ax>sin(x)$对于$x\in (0,\frac{\pi}{2})$恒成立,求$a$的取值范围。
(答案将会于稍晚些时候发布在评论区)
